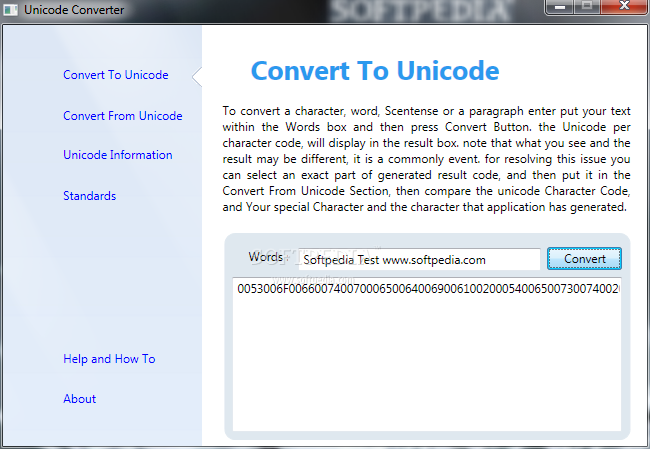
This is mandatory. Although the number might change for future versions of XML, 1.0 is the current version. The encoding declaration, encoding='UTF-8'? This is optional. If used, the encoding declaration must appear immediately after the version information in the XML declaration, and must contain a value representing an existing character. Chinese encoding conversion application. Chinese Encoding Converter is a handy, small, Java based tool specially designed to offer you a Chinese encoding conversion software.
When you’re doing supervised learning, you often have to deal with categorical variables. That is, variables which don’t have a natural numerical representation. The problem is that most machine learning algorithms require the input data to be numerical. At some point or another a data science pipeline will require converting categorical variables to numerical variables.
There are many ways to do so:
- Label encoding where you choose an arbitrary number for each category
- One-hot encoding where you create one binary column per category
- Vector representation a.k.a. word2vec where you find a low dimensional subspace that fits your data
- Optimal binning where you rely on tree-learners such as LightGBM or CatBoost
- Target encoding where you average the target value by category
Each and every one of these method has its own pros and cons. The best approach typically depends on your data and your requirements. If a variable has a lot of categories, then a one-hot encoding scheme will produce many columns, which can cause memory issues. In my experience, relying on LightGBM/CatBoost is the best out-of-the-box method. Label encoding is useless and you should never use it. However if your categorical variable happens to be ordinal then you can and should represent it with increasing numbers (for example “cold” becomes 0, “mild” becomes 1, and “hot” becomes 2). Word2vec and others such methods are cool and good but they require some fine-tuning and don’t always work out of the box.
Target encoding is a fast way to get the most out of your categorical variables with little effort. The idea is quite simple. Say you have a categorical variable $x$ and a target $y$ – $y$ can be binary or continuous, it doesn’t matter. For each distinct element in $x$ you’re going to compute the average of the corresponding values in $y$. Then you’re going to replace each $x_i$ with the according mean. This is rather easy to do in Python and the pandas library.
First let’s create some dummy data.
| $x_0$ | $x_1$ | $y$ |
|---|---|---|
| $a$ | $c$ | 1 |
| $a$ | $c$ | 1 |
| $a$ | $c$ | 1 |
| $a$ | $c$ | 1 |
| $a$ | $c$ | 0 |
| $b$ | $c$ | 1 |
| $b$ | $c$ | 0 |
| $b$ | $c$ | 0 |
| $b$ | $c$ | 0 |
| $b$ | $d$ | 0 |
We can start by computing the means of the $x_0$ column.
This results in the following dictionary.
We can then replace each value in $x_0$ with the matching mean.
We now have the following data frame.
| $x_0$ | $x_1$ | $y$ |
|---|---|---|
| 0.8 | $c$ | 1 |
| 0.8 | $c$ | 1 |
| 0.8 | $c$ | 1 |
| 0.8 | $c$ | 1 |
| 0.8 | $c$ | 0 |
| 0.2 | $c$ | 1 |
| 0.2 | $c$ | 0 |
| 0.2 | $c$ | 0 |
| 0.2 | $c$ | 0 |
| 0.2 | $d$ | 0 |
We can do the same for $x_1$.
| $x_0$ | $x_1$ | $y$ |
|---|---|---|
| 0.8 | 0.444 | 1 |
| 0.8 | 0.444 | 1 |
| 0.8 | 0.444 | 1 |
| 0.8 | 0.444 | 1 |
| 0.8 | 0.444 | 0 |
| 0.2 | 0.444 | 1 |
| 0.2 | 0.444 | 0 |
| 0.2 | 0.444 | 0 |
| 0.2 | 0.444 | 0 |
| 0.2 | 0 | 0 |
Target encoding is good because it picks up values that can explain the target. In this silly example value $a$ of variable $x_0$ has an average target value of $0.8$. This can greatly help the machine learning classifications algorithms used downstream.
The problem of target encoding has a name: over-fitting. Indeed, relying on an average value isn’t always a good idea when the number of values used in the average is low. You’ve got to keep in mind that the dataset you’re training on is a sample of a larger set. This means that whatever artifacts you may find in the training set might not hold true when applied to another dataset (i.e. the test set).
In the above xample, the value $d$ of variable $x_1$ is replaced with a 0 because it only appears once and the corresponding value of $y$ is a 0. Therefore, we’re over-fitting because we don’t have enough values to be sure that 0 is in fact the mean value of $y$ when $x_1$ is equal to $d$. In other words, relying on the average of only a few values is too reckless.
There are various ways to handle this. A popular way is to use cross-validation and compute the means in each out-of-fold dataset. This is what H20 does and what many Kagglers do too. Another approach which I much prefer is to use additive smoothing. This is supposedly what IMDB uses to rate its movies.
Text Encoding Converter
The intuition is as follows. Imagine a new movie is posted on IMDB and it receives three ratings. Taking into account the three ratings gives the movie an average of 9.5. This is surprising because most movies tend to hover around 7, and the very good ones rarely go above 8. The point is that the average can’t be trusted because there are too few values. The trick is to “smooth” the average by including the average rating over all movies. In other words, if there aren’t many ratings we should rely on the global average rating, whereas if there enough ratings then we can safely rely on the local average.
Mathematically this is equivalent to:
$$begin{equation}mu = frac{n times bar{x} + m times w}{n + m}end{equation}$$
where
- $mu$ is the mean we’re trying to compute (the one that’s going to replace our categorical values)
- $n$ is the number of values you have
- $bar{x}$ is your estimated mean
- $m$ is the “weight” you want to assign to the overall mean
- $w$ is the overall mean
In this notation, $m$ is the only parameter you have to set. The idea is that the higher $m$ is, the more you’re going to rely on the overall mean $w$. If $m$ is equal to 0 then you’re simply going to compute the empirical mean, which is:
$$begin{equation}mu = frac{n times bar{x} + 0 times w}{n + 0} = frac{n times bar{x}}{n} = bar{x}end{equation}$$
In other words you’re not doing any smoothing whatsoever.
Again this is quite easy to do in Python. First we’re going to write a method that computes a smooth mean. It’s going to take as input a pandas.DataFrame, a categorical column name, the name of the target column, and a weight $m$.
Let’s see what this does in the previous example with a weight of, say, 10.
| $x_0$ | $x_1$ | $y$ |
|---|---|---|
| 0.6 | 0.526316 | 1 |
| 0.6 | 0.526316 | 1 |
| 0.6 | 0.526316 | 1 |
| 0.6 | 0.526316 | 1 |
| 0.6 | 0.526316 | 0 |
| 0.4 | 0.526316 | 1 |
| 0.4 | 0.526316 | 0 |
| 0.4 | 0.526316 | 0 |
| 0.4 | 0.526316 | 0 |
| 0.4 | 0.454545 | 0 |
It’s quite noticeable that each computed value is much closer to the overall mean of 0.5. This is because a weight of 10 is rather large for a dataset of only 10 values. The value $d$ of variable $x_1$ has been replaced with 0.454545 instead of the 0 we got earlier. The equation for obtaining it was:
$$begin{equation}d = frac{1 times 0 + 10 times 0.5}{1 + 10} = frac{0 + 5}{11} simeq 0.454545end{equation}$$
Meanwhile the new value for replacing the value $a$ of variable $x_0$ was:
$$begin{equation}a = frac{5 times 0.8 + 10 times 0.5}{5 + 10} = frac{4 + 5}{15} = 0.6end{equation}$$
Computing smooth means can be done extremely quickly. What’s more, you only have to choose a single parameter, which is $m$. I find that setting to something like 300 works well in most cases. It’s quite intuitive really: you’re saying that you require that there must be at least 300 values for the sample mean to overtake the global mean. There are other ways to do target encoding that are somewhat popular on Kaggle, such as this one. However, the latter method produces encoded variables which are very correlated with the output of additive smoothing, at the cost of requiring two parameters.
I’m well aware that there are many well-written posts about target encoding elsewhere. I just want to do my bit and help spread the word: don’t use vanilla target encoding! Go Bayesian and use priors. For those who are interested in using a scikit-learn compatible implementation, I did that just here.
Although the Mongolian Information Processing works began from 1980's, because of the standardization of the Mongolian have not been completed well, a lot kinds of The Mongolian Information Processing works have been delayed and the level is very low, we can say we are still standing at the beginning point of the Mongolian Information Processing world. Currently, we are all connected by internet and our daily life deeply depends on the digital world. The Mongolian digitization or Information Processing will be widely required by our Mongolians. The main problem of the Mongolian Information Processing is the Standardization of the Encoding. There are a lot kinds of Mongolian System in Inner Mongolia, Mongolia, and other countries or regions. But most of currently existing Mongolian system defined their own encoding code and different from each other. The contents and the texts created by each individual system hard to convert to other system and we can not use these kind on Mongolian System to communicate on Internet.
We can not share our techniques and knowledge by these Mongolian System. It is very important to use Unicode Standards to unify the Mongolian Encoding quickly. Unicode Mongolian Standards.
Free Download Mongolian Cyrillic converter 1.1.0.0 - A simple tool for turning regular text to or from Mongolian Cyrillic characters.
Encoding Converter Online
Unicode Standards is a global encoding standards which is accepted by all of the OS Venders and System makers. In the early 2000, The Mongolian Unicode Proposal had been accepted by the ISO Organization and Unicode Consortium. Just because of the implementation method of the Mongolian Unicode is very difficult and not exist till the Windows Vista support it by OpenType Font rendering techniques. Now, the Unicode Mongolian Encodings, can be supported by OpenType Font rendering techniques on Windows, Linux & Unix. And by AAT Font rendering techniques on Mac OS X, iOS.

The Mongolian Font is the script used by Mongolain Peoples from 13th Century. It is actually an alphabetic script, but the Mongolian have a special writing style. Firstly, the Mongolian write in vertical line and the line feed direction is from left to right. This writing style is all different from other languages existing on the world. It is different with the Chinese and Japanese Vertical Line mode.
Mongolian Encoding Converter 1.0 Download
Secondly, the Mongolian alphabet will be writing as continuously in a word. All of the alphabet, will be changed to different glyph to write at a word beginning, in a word between other alphabet, or at the word final position. For this reason, the Mongolian alphabet at least have 4 presentation glyphs, Isolate, Initial, Medial, and Final presentation glyph. Some of them have other special glyphs additionally. Currently, we have Unicode Mongolian Standards which is encoded by the Mongolian Alphabets. For displaying the Mongolian correctly, we have to change the alphabet to proper presentation glyph in the text. Pulse of life bracelet.
For support this kinds of glyph change requirements, Microsoft and Adobe defined a new Font Specification - font techiniqes and Apple defined their own Specification font techniques. The OpenType font mostly used on Microsoft windows and Linux & Unix Systems. The AAT font mostly used on Apple products like Mac OS X and iOS used on smart phone or tablet like iPhone, iPad, and iPod Touch. We are strongly promote the Unicode Mongolian Standards for unifying the Mongolian system encodings to make our Mongolian digital worlds will be able to communicate each other directly.
Mongolian Encoding Converter 1.00
This Mongolian Font site will provide necessary Fonts, Techniques and Applications for Unicode Mongolian Standards. Please feel free to download and utilize it. If you have any additional questions or advices, please let us know. The Unicode Mongolian on Windows XP If you are using Windows XP, please download the package bellow, and install under the instruction in readme.txt.